什么是递归
在函数中存在着调用函数本身的情况,这种现象就叫递归。递归和栈有紧密关联。我们可以将递归看做一次次入栈出栈的过程。
特点:
- 递归就是方法里调用自身。
- 在使用递增归策略时,必须有一个明确的递归结束条件,称为递归出口。
- 递归算法解题通常显得很简洁,但递归算法解题的运行效率较低。所以一般不提倡用递归算法设计程序。
- 在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成栈溢出等,所以一般不提倡用递归算法设计程序。
汉诺塔问题
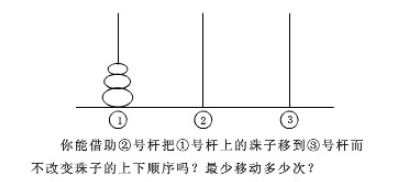
void hanoi(int n,int p1,int p2,int p3)
{
if(1==n)
cout<<"盘子从"<<p1<<"移到"<<p3<<endl;
else
{
hanoi(n-1,p1,p3,p2);
cout<<"盘子从"<<p1<<"移到"<<p3<<endl;
hanoi(n-1,p2,p1,p3);
}
}单一的递归用的很少,更多的是与一些其他算法思想结合在一起
递归和回溯
回溯:
把问题分步解决,在每一步都试验所有的可能,当发现已经找到一种方式或者目前这种方式不可能是结果的时候,退回上一步继续尝试其他可能。
当回溯用于树的时候,就是深度优先搜索。当然了,几乎所有可以用回溯解决的问题都可以表示为树。
递归是一种算法结构,而回溯包括后面的剪枝是一种算法思想。
全排列问题
把 $1 \sim n$ 这 $n$ 个整数排成一行后随机打乱顺序,输出所有可能的次序。
输入格式
一个整数 $n$。
输出格式
按照从小到大的顺序输出所有方案,每行 $1$ 个。
首先,同一行相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面。
数据范围
$1 \le n \le 9$
输入样例:
3输出样例:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1题解:
十分经典的dfs,选与不选的题。
看一下递归树
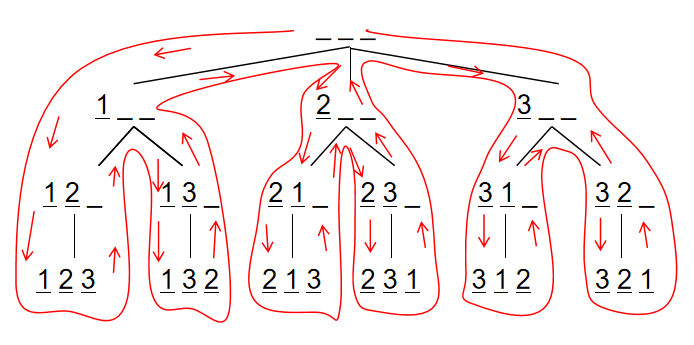
假设有 3 个空位,从前往后填数字,每次填一个位置,填的数字不能和前面一样。
最开始的时候,三个空位都是空的:__ __ __
首先填写第一个空位,第一个空位可以填 1,填写后为:1 __ __
填好第一个空位,填第二个空位,第二个空位可以填 2,填写后为:1 2 __
填好第二个空位,填第三个空位,第三个空位可以填 3,填写后为: 1 2 3
这时候,空位填完,无法继续填数,所以这是一种方案,输出。
然后往后退一步,退到了状态:1 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3 ,没有其他数字可以填。
因此再往后退一步,退到了状态:1 __ __。第二个空位上除了填过的 2,还可以填 3。第二个空位上填写 3,填写后为:1 3 __
填好第二个空位,填第三个空位,第三个空位可以填 2,填写后为: 1 3 2
这时候,空位填完,无法继续填数,所以这是一种方案,输出。
然后往后退一步,退到了状态:1 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2,没有其他数字可以填。
因此再往后退一步,退到了状态:1 __ __。第二个空位上除了填过的 2,3,没有其他数字可以填。
因此再往后退一步,退到了状态:__ __ __。第一个空位上除了填过的 1,还可以填 2。第一个空位上填写 2,填写后为:2 __ __
填好第一个空位,填第二个空位,第二个空位可以填 1,填写后为:2 1 __
填好第二个空位,填第三个空位,第三个空位可以填 3,填写后为:2 1 3
这时候,空位填完,无法继续填数,所以这是一种方案,输出。
然后往后退一步,退到了状态:2 1 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3,没有其他数字可以填。
因此再往后退一步,退到了状态:2 __ __。第二个空位上除了填过的 1,还可以填 3。第二个空位上填写 3,填写后为:2 3 __
填好第二个空位,填第三个空位,第三个空位可以填 1,填写后为:2 3 1
这时候,空位填完,无法继续填数,所以这是一种方案,输出。
然后往后退一步,退到了状态:2 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 1,没有其他数字可以填。
因此再往后退一步,退到了状态:2 __ __。第二个空位上除了填过的 1,3,没有其他数字可以填。
因此再往后退一步,退到了状态:__ __ __。第一个空位上除了填过的 1,2,还可以填 3。第一个空位上填写 3,填写后为:3 __ __
填好第一个空位,填第二个空位,第二个空位可以填 1,填写后为:3 1 __
填好第二个空位,填第三个空位,第三个空位可以填 2,填写后为:3 1 2
这时候,空位填完,无法继续填数,所以这是一种方案,输出。
然后往后退一步,退到了状态:3 1 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2,没有其他数字可以填。
因此再往后退一步,退到了状态:3 __ __。第二个空位上除了填过的 1,还可以填 2。第二个空位上填写 2,填写后为:3 2 __
填好第二个空位,填第三个空位,第三个空位可以填 1,填写后为:3 2 1
这时候,空位填完,无法继续填数,所以这是一种方案,输出。
然后往后退一步,退到了状态:3 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 1,2,没有其他数字可以填。
因此再往后退一步,退到了状态:3 __ __。第二个空位上除了填过的 1,2,没有其他数字可以填。
因此再往后退一步,退到了状态:__ __ __。第一个空位上除了填过的 1,2,3,没有其他数字可以填。
此时深度优先搜索结束,输出了所有的方案。
#include<iostream>
using namespace std;
const int N = 10;
int path[N]; //保存序列
int state[N]; //数字是否被用过
int n;
void dfs(int u)
{
if(u > n) //数字填完了,输出
{
for(int i = 1; i <= n; i++) //输出方案
cout << path[i] << " ";
cout << endl;
}
for(int i = 1; i <= n; i++) //空位上可以选择的数字为:1 ~ n
{
if(!state[i]) //如果数字 i 没有被用过
{
path[u] = i; //放入空位
state[i] = 1; //数字被用,修改状态
dfs(u + 1); //填下一个位
state[i] = 0; //回溯,取出 i
}
}
}
int main()
{
cin >> n;
dfs(1);
return 0;
}
类似的题:
集合的子集
#include<iostream>
#include<vector>
using namespace std;
const int N = 12;
int a[N];
int n;
vector<int> v;
void dfs(int curr,int n) //curr搜索到数组的哪一个位置,n表示数组长度
{
if(curr==n) //curr==n到头了,输出
{
for(int i = 0;i<v.size();i++) cout<<v[i];
cout<<endl;
return;
}
v.push_back(a[curr]); //选当前的数,压入vector
dfs(curr+1,n);
v.pop_back(); //回溯,取出上一个压进去的数
dfs(curr+1,n);
}
int main()
{
cin>>n;
for(int i = 0;i<n;i++) cin>>a[i];
dfs(0,n);
} 数的划分
题目描述
将整数 $n$ 分成 $k$ 份,且每份不能为空,任意两个方案不相同(不考虑顺序)。 例如:$n=7$,$k=3$,下面三种分法被认为是相同的。 $1,1,5$; $1,5,1$; $5,1,1$. 问有
多少种不同的分法。
输入格式
$n,k$ ($6<n \le 200$,$2 \le k \le 6$)
输出格式
$1$ 个整数,即不同的分法。
输入样例
7 3输出样例
4说明
四种分法为: $1,1,5$; $1,2,4$; $1,3,3$; $2,2,3$.
题解:
这道理就是暴力搜索,为了防止有重复的答案,我们按着从小到大的顺序进行搜索。从 $1$ 开始搜索,每次加 $1$ ,搜到 $k$ 个数时,判断是否等于 $n$ ,是,则答案 $+1$ ,然后返回。
我们 $i$ 是从 $1$ 开始,到哪结束呢?以后的数会越来越大,所以只要枚举到sum+i*(k-cur)<=n就可以了,比i<=n节约了不少时间和空间。
#include<iostream>
using namespace std;
int n,k,cnt;
void dfs(int last,int sum,int cur) //last表示现在搜到哪个数,sum是搜到的数相加的和,cur是现在搜到数的个数
{
if(cur==k)
{
if(sum==n) cnt++;
return;
}
for(int i=last;sum+i*(k-cur)<=n;i++) //剪枝,只用枚举到sum+i*(k-cur)<=n为止
dfs(i,sum+i,cur+1);
}
int main()
{
cin>>n>>k;
dfs(1,0,0);
cout<<cnt;
}未完待续。。。

